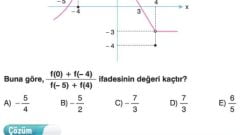
İşlemlerle Cebirsel Düşünme 5. Sınıf Matematik
Eşitliğin korunumu ve işlem özellikleri, işlem önceliği, sayı ve şekil örüntüleri, temel aritmetik işlemler konularını içeren kapsamlı matematik açıklamaları ve örnekleri. Öğrenciler için matematiksel kavramları anlamak ve problem çözme yeteneklerini geliştirmek amacıyla hazırlanmış eğitim içerikleri. Eşitlik korunumu, toplama, çıkarma, çarpma ve bölme işlemlerinin özellikleri, işlem önceliği kuralları ve örnekler, sayı ve şekil örüntülerinin görsellerle desteklenmiş anlatımları. Temel matematik becerilerini güçlendirmek ve öğrenmeyi kolaylaştırmak için ideal bir kaynak.
İşlemlerle Cebirsel Düşünme Konuları
5. Sınıf İşlemlerle Cebirsel Düşünme konu anlatımı, etkinlikler
Temel Kavramlar
Değişkenler ve Sabitler
- Değişken: Değişken, farklı değerler alabilen bir semboldür. Genellikle harflerle (x, y, z) gösterilir.
- Sabit: Sabit, değeri değişmeyen bir sayıdır.
Cebirsel İfadeler
Cebirsel ifadeler, sayıların ve değişkenlerin bir araya gelmesiyle oluşur. Örneğin, 2x + 3 bir cebirsel ifadedir.
- Terim: Bir cebirsel ifadedeki her bir bileşen (örneğin, 2x ve 3).
- Katsayı: Değişkenin önündeki sayı (örneğin, 2x ifadesinde 2).
İşlemler ve Cebirsel İfadeler
- Toplama ve Çıkarma: Cebirsel ifadelerde toplama ve çıkarma işlemleri terimler üzerinde yapılır. Örneğin, 2x + 3x = 5x.
- Çarpma ve Bölme: Cebirsel ifadelerde çarpma ve bölme işlemleri katsayılar ve değişkenler üzerinde yapılır. Örneğin, 3x * 2 = 6x.
Cebirsel Düşünme
Cebirsel İfadeleri Anlama Öğrenciler, cebirsel ifadeleri anlamayı ve bu ifadelerle işlem yapmayı öğrenirler. Örneğin, 2x + 5 ifadesinin x = 3 için değerini bulma.
Örnek Problem: 2x + 5 ifadesinde x = 3 ise, ifadenin değeri nedir?
Çözüm: 2(3) + 5 = 6 + 5 = 11
Denklem Çözme Denklem çözme, bir cebirsel ifadede değişkenin değerini bulma işlemidir. Örneğin, 2x + 3 = 11 denklemini çözme.
Örnek Problem: 2x + 3 = 11 denklemini çözünüz.
Çözüm: 2x + 3 = 11 => 2x = 8 => x = 4
Cebirsel İlişkileri Kullanma Cebirsel düşünme, öğrencilerin matematiksel ilişkileri anlamalarını ve kullanmalarını sağlar. Örneğin, bir problemde toplamın nasıl ifade edileceği.
Örnek Problem: Bir kutuda x kadar kalem var ve her bir öğrencinin 3 kalemi var. Tüm öğrencilerin kalemlerinin toplamı nasıl ifade edilir?
Çözüm: 3x
Gerçek Yaşam Problemleri
Cebirsel düşünme, öğrencilerin günlük yaşamda karşılaştıkları problemleri çözmelerine yardımcı olur. İşte bazı örnekler:
1. Alışveriş Problemi
Problem: Bir mağazada bir tişört x TL ve bir pantolon 2x TL'dir. Ali'nin 5x TL'si var. Ali kaç tişört ve kaç pantolon alabilir?
Çözüm: Ali'nin 5x TL'si olduğu için, 1 tişört ve 2 pantolon alabilir (x + 2x + 2x = 5x).
2. Bahçe Problemi
Problem: Bir bahçede 3y kadar çiçek var ve her sıra y kadar çiçek içeriyor. Bahçede kaç sıra çiçek var?
Çözüm: Bahçede 3 sıra çiçek var (3y / y = 3).
3. Yemek Tarifi Problemi
Problem: Bir kek tarifinde 2x kadar şeker ve x kadar un kullanılıyor. 3 kek yapmak için ne kadar şeker ve un gerekir?
Çözüm: 6x kadar şeker ve 3x kadar un gerekir (2x * 3 ve x * 3).
Etkinlik 1: Değişken Kartları
- Amaç: Öğrencilerin değişkenleri anlamalarını sağlamak.
- Uygulama: Değişken ve sabit kartları hazırlayın. Öğrencilerden bu kartları kullanarak cebirsel ifadeler oluşturmalarını isteyin.
Etkinlik 2: Denklem Çözme Oyunu
- Amaç: Öğrencilerin denklemleri çözme becerilerini geliştirmek.
- Uygulama: Basit denklemler içeren kartlar hazırlayın. Öğrencilerden bu kartlardaki denklemleri çözmelerini isteyin.
Etkinlik 3: Gerçek Yaşam Problemleri ile Cebir Çalışması
- Amaç: Öğrencilerin cebirsel düşünme becerilerini günlük yaşamda kullanmalarını sağlamak.
- Uygulama: Alışveriş, bahçe veya yemek tarifi gibi gerçek yaşam problemleri içeren etkinlikler düzenleyin.
5. sınıf matematik müfredatında işlemlerle cebirsel düşünme, öğrencilerin matematiksel ifadeleri anlama ve kullanma becerilerini geliştirmeyi amaçlar. Değişkenler, sabitler, cebirsel ifadeler ve denklemler gibi temel kavramlar, öğrencilerin problem çözme yeteneklerini artırır. Bu makalede ele alınan konular, örnek problemler ve etkinlikler, öğrencilerin cebirsel düşünme becerilerini pekiştirmelerine yardımcı olacaktır. Cebirsel düşünme, öğrencilerin matematiksel ilişkileri anlamalarını ve günlük yaşamda karşılaştıkları problemleri çözmelerini sağlar, böylece ileri düzey matematik konularına hazırlık niteliğindedir.