8. Sınıf Kareköklü İfadeler Konu Anlatımı Matematik

Tam Kare Pozitif Tam Sayılar ile Bu Sayıların Karekökleri Arasındaki İlişki

Tam Kare Pozitif Tam Sayılar ile Bu Sayıların Karekökleri Arasındaki İlişki Çözümlü Sorular

Tam Kare Olmayan Sayıların Karekök Değerlerinin Aralıkları

Tam Kare Olmayan Sayıların Karekök Değerlerinin Aralıkları Çözümlü Sorular

Kareköklü Bir İfadeyi a√b Şeklinde Yazma ve a√b Şeklindeki İfadede Katsayıyı Karekök İçine Alma

Kareköklü Bir İfadeyi a√b Şeklinde Yazma ve a√b Şeklindeki İfadede Katsayıyı Karekök İçine Alma
Çözümlü Sorular

Kareköklü İfadelerde Çarpma İşlemi

Kareköklü İfadelerde Bölme İşlemi

Kareköklü İfadelerde Çarpma ve Bölme İşlemleri Çözümlü Sorular

Kareköklü İfadelerde Toplama ve Çıkarma İşlemleri

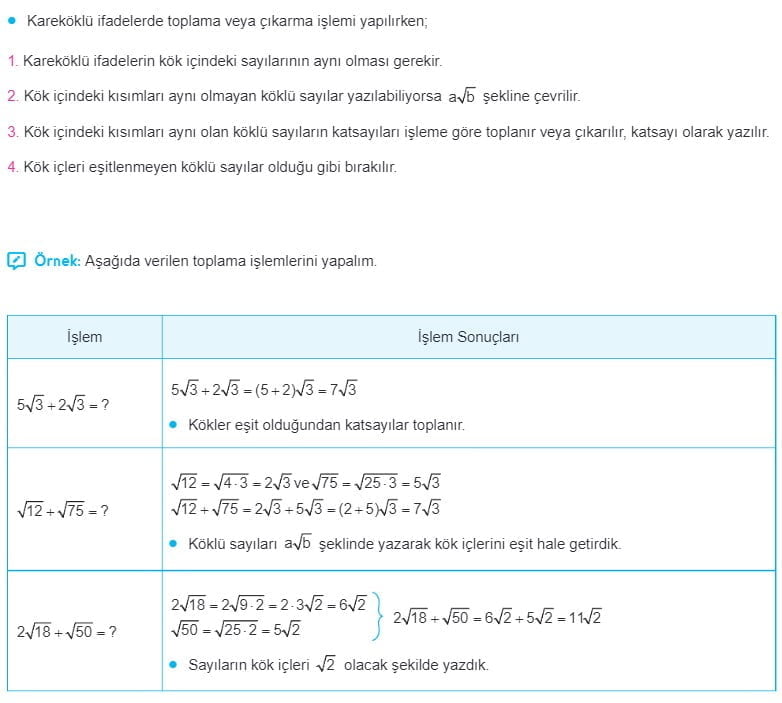
Kareköklü İfadelerde Toplama ve Çıkarma İşlemleri Çözümlü Sorular

Kareköklü Bir İfade ile Çarpıldığında Sonucu Bir Doğal Sayı Yapan Çarpanlar

Kareköklü Bir İfade ile Çarpıldığında Sonucu Bir Doğal Sayı Yapan Çarpanlar Çözümlü Sorular

Ondalık İfadelerin Karekökleri

Ondalık İfadelerin Karekökleri Çözümlü Sorular

Gerçek Sayılar

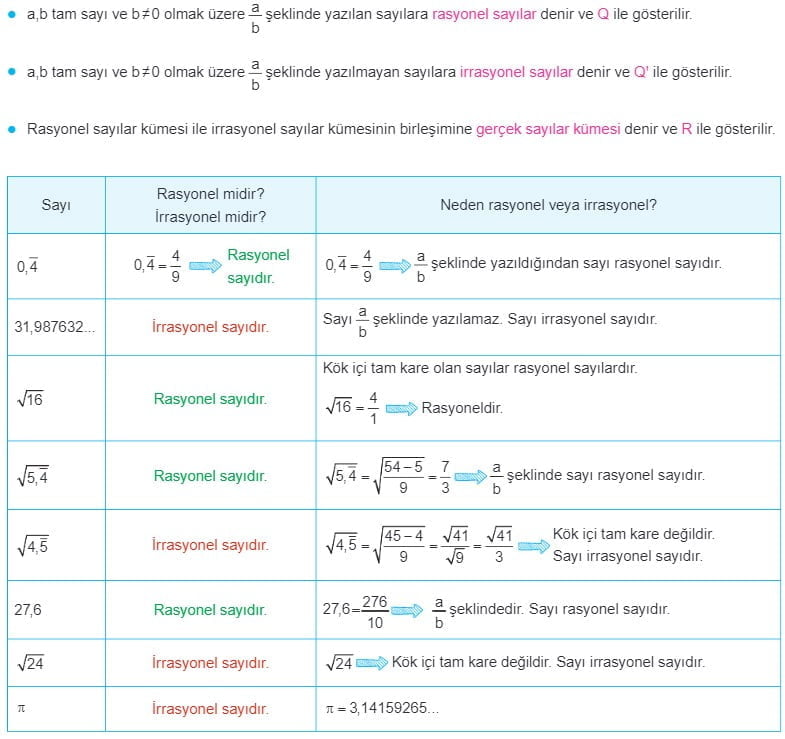
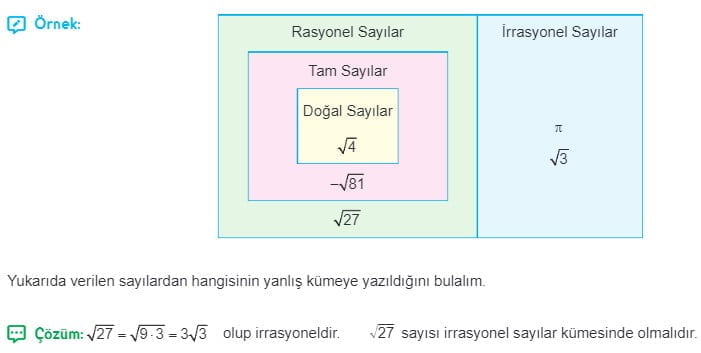
Gerçek Sayılar Çözümlü Sorular

Kareköklü İfadeler Video

Kareköklü İfadeler:

Kareköklü ifadeler, bir sayının karesi olarak ifade edilebilen ifadelerdir. Karekök, bir sayının karesi olan pozitif sayıyı ifade eder. Karekök işareti (√) bu işlemi temsil eder. Karekök işareti altındaki sayıya ise "radikand" denir. İşte kareköklü ifadelerin temel kuralları ve özellikleri:

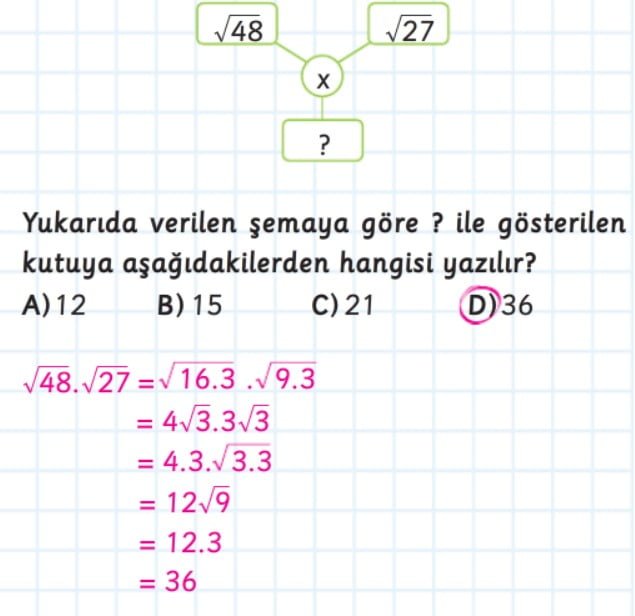
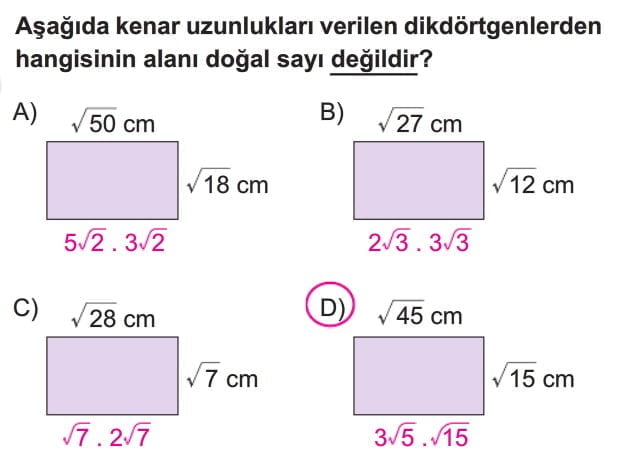
1. √a * √b = √(a * b): Karekök işareti altındaki iki sayının çarpımı, bu iki sayının karekökünün çarpımına eşittir.
2. √(a / b) = √a / √b: Karekök işareti altındaki iki sayının bölümü, bu iki sayının karekökünün bölümüne eşittir.
3. √(a^2) = a: Bir sayının karesinin karekökü, o sayının kendisine eşittir.
4. √(a * a) = |a|: Bir sayının karesinin karekökü, o sayının mutlak değerine (pozitif değerine) eşittir.
5. √0 = 0: Sıfırın karekökü her zaman sıfırdır.
6. √1 = 1: Bir'in karekökü her zaman birdir.

Kareköklü ifadeler, özellikle geometri, trigonometri, ve denklem çözme gibi matematiksel konularda yaygın olarak kullanılır. Karekök işlemi, bir sayının pozitif karekökünü hesaplamak için kullanılır ve bu, özellikle uzunluğu veya alanı ifade etmek için önemlidir. Öğrenciler, kareköklü ifadeleri sadeleştirme ve hesaplama becerilerini geliştirerek matematiksel düşünme yeteneklerini artırabilirler.

Çözümlü Soru 1: √12 ifadesini sadeleştirin ve sonucu bulun.

Çözüm 1: √12 ifadesini sadeleştirmek için önce 12'nin çarpanlarını bulalım. 12 = 2 * 2 * 3 olarak faktörlerine ayrılabilir.

√12 = √(2 * 2 * 3)

√12 = √(2^2 * 3)

Şimdi karekök işlemi ve çarpanları ayırdığımız için ifadeyi daha basit bir şekilde yazabiliriz:

√(2^2) * √3 = 2√3

Sonuç: √12 = 2√3

Çözümlü Soru 2: √48 ifadesini sadeleştirin ve sonucu bulun.

Çözüm 2: √48 ifadesini sadeleştirmek için önce 48'in çarpanlarını bulalım. 48 = 2 * 2 * 2 * 2 * 3 olarak faktörlerine ayrılabilir.

√48 = √(2 * 2 * 2 * 2 * 3)

√48 = √(2^4 * 3)

Şimdi karekök işlemi ve çarpanları ayırdığımız için ifadeyi daha basit bir şekilde yazabiliriz:

√(2^4) * √3 = 4√3

Sonuç: √48 = 4√3

Etkinlik Önerisi: Kareköklü İfadeler Yarışması Öğrencilere farklı kareköklü ifadeler verin ve bu ifadeleri sadeleştirmelerini veya sonuçlarını bulmalarını isteyin. Öğrenciler gruplar halinde veya bireysel olarak yarışabilirler. Doğru cevapları hızlıca bulmaya çalışsınlar.

Etkinlik Önerisi: Kareköklü İfadelerin Uygulamaları Öğrencilere kareköklü ifadelerin günlük yaşamdaki uygulamalarını araştırmalarını isteyin. Örneğin, bir üçgenin hipotenüsünü hesaplarken nasıl kareköklü ifadeler kullanıldığını veya bir kare alanın kenar uzunluğunu hesaplarken nasıl kareköklü ifadelere ihtiyaç duyulduğunu inceleyebilirler. Ardından, buldukları bilgileri sınıfta paylaşabilirler.

Kareköklü ifadeler, matematikte önemli bir konsepttir ve genellikle matematiksel problemleri çözme, özellikle geometri ve trigonometri gibi alanlarda kullanılır. Bu tür etkinlikler, öğrencilerin bu konsepti anlamalarına ve uygulamalarına yardımcı olabilir.

Problem 1: Bir dik üçgenin iki kenarının uzunluğu sırasıyla √2 ve √3 birimdir. Bu üçgenin hipotenüsünün uzunluğunu bulun.

Çözüm 1: Hipotenüsün uzunluğunu bulmak için Pisagor Teoremi'ni kullanabiliriz. Pisagor Teoremi şu şekildedir: Hipotenüsün karesi, diğer iki kenarın karelerinin toplamına eşittir.

Hipotenüs^2 = (√2)^2 + (√3)^2 Hipotenüs^2 = 2 + 3 Hipotenüs^2 = 5

Hipotenüs = √5 birim.

Problem 2: Bir dairenin yarı çapı √10 birimdir. Bu dairenin alanını bulun.

Çözüm 2: Dairenin alanını hesaplamak için A = πr^2 formülünü kullanabiliriz, burada r dairenin yarı çapını temsil eder.

A = π(√10)^2 A = π * 10 A = 10π birim kare.

Problem 3: √7 ve √5 ifadelerinin toplamını ve farkını bulun.

Çözüm 3: Toplam: √7 + √5 Fark: √7 - √5

Bu ifadeler sadeleştirilmez, çünkü √7 ve √5, farklı irrasyonel sayılardır ve bu ifadeler üzerinde başka bir işlem yapılamaz. Bu nedenle sonuçlar şu şekildedir:

Toplam: √7 + √5 Fark: √7 - √5

Kareköklü sayılar, özellikle geometri ve trigonometri gibi matematik konularında sıkça karşımıza çıkar. Bu problemler, öğrencilere kareköklü sayıları anlama ve kullanma becerisi kazandırmaya yardımcı olur.

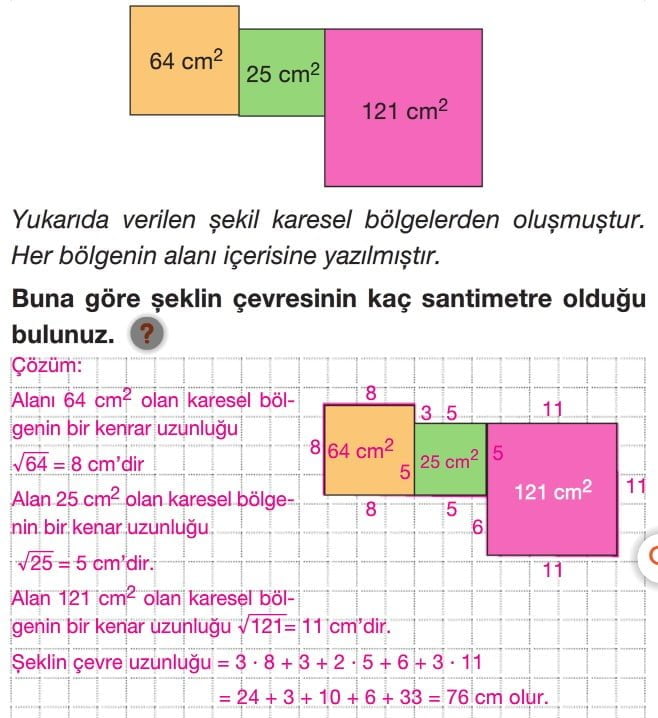
Tam kare pozitif tam sayılar, karelerin sonuçları olarak ortaya çıkan sayılardır. Örnek olarak, 1, 4, 9, 16, 25 gibi sayılar tam kare pozitif tam sayılardır. Bu sayıların karekökleri, yani bu sayılara ulaşmak için kaçıncı dereceden kök almanız gerektiğini ifade eden sayılar da vardır.

Örneğin, 1 sayısının karekökü 1'dir, çünkü 1 x 1 = 1. 4 sayısının karekökü 2'dir, çünkü 2 x 2 = 4. 9 sayısının karekökü 3'tür, çünkü 3 x 3 = 9. Benzer şekilde, 16 sayısının karekökü 4'tür ve 25 sayısının karekökü de 5'tir.

Bu ilişki, kareköklerin tam kare pozitif tam sayıların karelerinin kökleri olduğunu gösterir. Karekökler, bir sayının karesini elde etmek için kullanılabilir. Örneğin, 9 sayısının karesini elde etmek isterseniz, 9'un karekökü olan 3'ü kullanarak 3 x 3 = 9 sonucuna ulaşabilirsiniz.

Bu ilişki, matematikte önemlidir çünkü kareköklerin ve karelerin birçok uygulama alanında kullanımı vardır. Özellikle geometri, fizik, mühendislik ve istatistik gibi bilim ve mühendislik alanlarında sık sık karşınıza çıkar. Tam kare pozitif tam sayılar ve karekökleri, sayılar arasındaki bu önemli ilişkiyi anlamak için temel bir kavramdır.

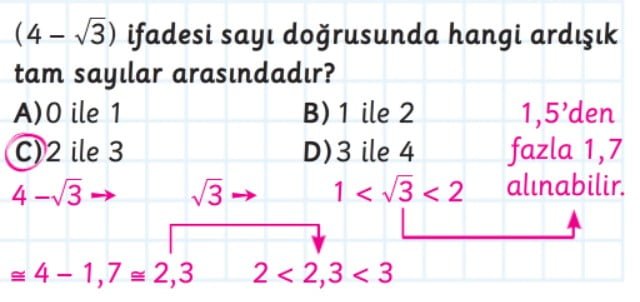
Tam kare olmayan sayıların karekök değerleri genellikle ondalık kesirlerle ifade edilir. Karekökler, tam kare pozitif tam sayıların kareköklerinden farklıdır ve bu sayıların özgün özelliklerini yansıtır. Karekök değerlerinin aralıkları farklı sayılar için farklıdır, ancak genel olarak şu şekildedir:

1. İki tam kare pozitif tam sayı arasındaki karekök değerleri birbirine daha yakındır. Örneğin, 9 ve 16 arasındaki tam kare pozitif tam sayılar 3 ve 4'tür. Bu nedenle 9 ile 16 arasındaki sayıların karekök değerleri 3 ile 4 arasındadır.
2. Tam kare pozitif tam sayılara yakın olan tam kare olmayan sayıların karekökleri daha büyük ondalık kesir değerlerine sahiptir. Örneğin, 12 sayısı 9 ile 16 arasında bir sayıdır ve karekökü yaklaşık olarak 3.464'dür.
3. Tam kare pozitif tam sayılara uzak olan tam kare olmayan sayıların karekökleri daha büyük ondalık kesir değerlerine sahiptir. Örneğin, 30 sayısı 25 ile 36 arasında bir sayıdır ve karekökü yaklaşık olarak 5.477'dir.
4. Karekök değerleri arasındaki farklar tam kare pozitif tam sayılar arasındaki farklar kadar büyük değildir. Örneğin, 9 ve 16 arasındaki tam kare pozitif tam sayılar arasındaki fark 7 iken, bu iki sayının karekökleri arasındaki fark yaklaşık olarak 1. İki ardışık tam kare pozitif tam sayının karekökleri arasındaki farklar giderek azalır.

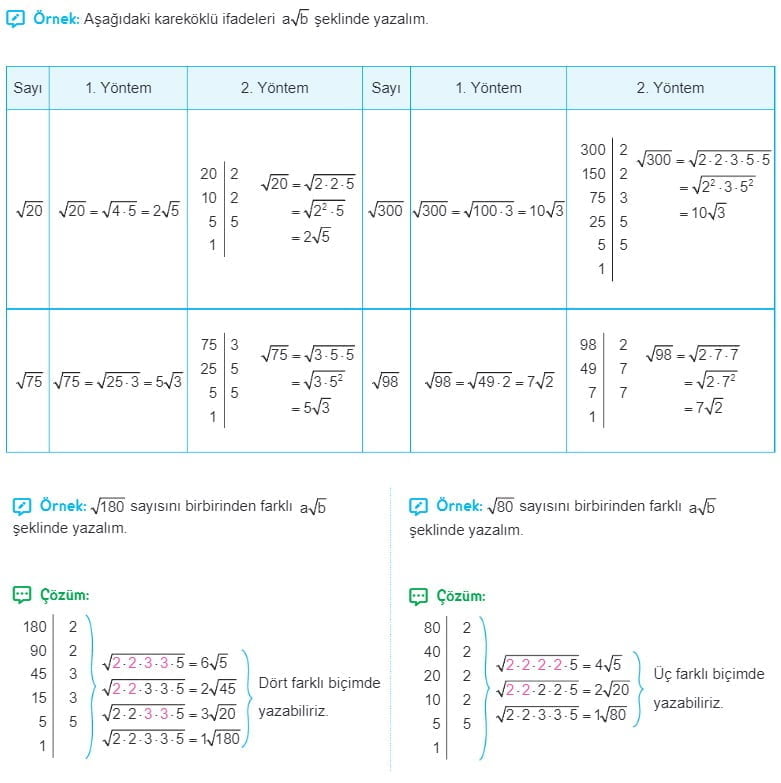
Kareköklü bir ifadeyi a√b şeklinde yazmak, bir sayının karekökü olan √b ile bir sayının katsayısı olan a'nın çarpımıdır. Ancak bazen a'nın √b içine alınması gerekebilir. İşte a√b şeklindeki ifadenin a'yı √b içine alma işlemi:

1. İlk olarak, a√b ifadesini inceleyin. Örneğin, 2√3 şeklinde bir ifade olsun.
2. Bu ifadedeki a'yı √b içine almak istiyorsanız, a'yı √b ile çarpın. Yani, 2√3 ifadesindeki 2'yi √3 ile çarpın.
3. Sonuç olarak elde edeceğiniz ifade, a√b'nin a'yı √b içine almış hali olacaktır. Yani, 2√3 ifadesinde 2'yi √3 ile çarptığınızda sonuç √(2*3) = √6 olur.

Sonuç olarak, 2√3 ifadesini √6 şeklinde yazmış olursunuz. Bu, a'nın √b içine alınmış hali olarak ifade edilir. Bu işlem, özellikle matematiksel ifadeleri daha basit ve sade bir hale getirmenize yardımcı olabilir.